Bitcoin: Ein elektronisches Peer-to-Peer-Cash-System

Satoshi Nakamoto
satoshin@gmx.com
www.bitcoin.org

Abstrakt. Ein reine Peer-to-Peer-Version elektronischen Cashs würde es ermöglichen, Onlinezahlungen ohne Rückgriff auf ein Finanzinstitut direkt von einer Partei zur anderen zu senden. Digitale Signaturen stellen einen Teil der Lösung bereit, doch die wichtigsten Vorteile gehen verloren, wenn dennoch eine vertrauenswürdige dritte Partei vonnöten ist, um Doppelausgaben zu verhindern. Wir schlagen eine Lösung des Doppelausgabenproblems durch die Verwendung eines Peer-to-Peer-Netzwerks vor. Das Netzwerk zeitstempelt Transaktionen, indem es sie in eine fortlaufende Kette aus hashwertbasierten Arbeitsnachweisen hasht, wodurch ein Verlauf geschaffen wird, der nicht geändert werden kann, ohne den Arbeitsnachweis erneut zu erbringen. Die längste Kette stellt nicht nur den Beweis der Sequenz aller bezeugten Ereignisse dar, sondern zudem den Nachweis, dass sie vom größten Pool an CPU-Leistung stammt. Solange der Großteil der CPU-Leistung von Nodes stammt, die nicht bei einem Angriff auf das Netzwerk kooperieren, werden sie die längste Kette erzeugen und die Angreifer abschütteln. Das Netzwerk selbst benötigt eine minimale Struktur. Nachrichten werden auf der Grundlage bestmöglichen Bemühens übermittelt und Nodes können das Netzwerk beliebig verlassen oder ihm beitreten, wobei sie die längste Arbeitsnachweiskette als Beweis dafür akzeptieren, was während ihrer Abwesenheit passierte.

1. Einführung

Der Internethandel ist inzwischen fast vollständig von Finanzinstituten abhängig, die als vertrauenswürdige Dritte elektronische Zahlungen abwickeln. Während dieses System für die meisten Transaktionen angemessen funktioniert, leidet es dennoch unter den inhärenten Schwächen des vertrauensbasierten Modells. Nicht rückgängig zu machende Transaktionen sind nicht wirklich realisierbar, da Finanzinstitute dazu gezwungen sind, bei Streitigkeiten zu vermitteln. Die Kosten der Konfliktlösung erhöht die Transaktionskosten, was die kleinste praktikable Transaktionsgröße und damit die Möglichkeit kleiner, gelegentlicher Transaktionen einschränkt. Dazu kommen die allgemeineren Kosten des Verlustes der Fähigkeit, irreversible Zahlungen für irreversible Dienstleistungen tätigen zu können. Mit der Möglichkeit einer Rückgängigmachung breitet sich die Notwendigkeit des Vertrauens aus. Händler müssen ihren Kunden gegenüber argwöhnisch sein und ihnen mehr Informationen abverlangen, als sie ansonsten benötigten. Ein gewisser Anteil an Betrügerei wird als unausweichlich hingenommen. Diese Kosten und Zahlungsunsicherheiten können bei persönlichen Interaktionen durch die Verwendung von Bargeld vermieden werden, doch es existiert kein Mechanismus, der Zahlungen ohne vertrauenswürdige Dritte über Kommunikationskanäle ermöglichte.

Was notwendig ist, ist ein Zahlungssystem, das auf kryptographischen Nachweisen statt Vertrauen beruht und es zwei so geneigten Parteien ermöglicht, direkt und ohne Rückgriff auf eine vertrauenswürdige dritte Partei Transaktionen untereinander abzuwickeln. Transaktionen, die praktisch nicht rückgängig gemacht werden können, schützten Verkäufer vor Betrug, während übliche Treuhanddienste leicht implementiert werden könnten, um Käufer zu schützen. In dieser Arbeit schlagen wir eine Lösung des Doppelausgabenproblems vor, bei welcher ein Peer-to-Peer-verteilter Zeitstempelserver benutzt wird, um einen rechnergestützten Nachweis der chronologischen Reihenfolge von Transaktionen zu erzeugen. Das System ist sicher, solange ehrliche Nodes kollektiv mehr CPU-Leistung kontrollieren als jede kooperierende Gruppe angreifender Nodes.

2. Transaktionen

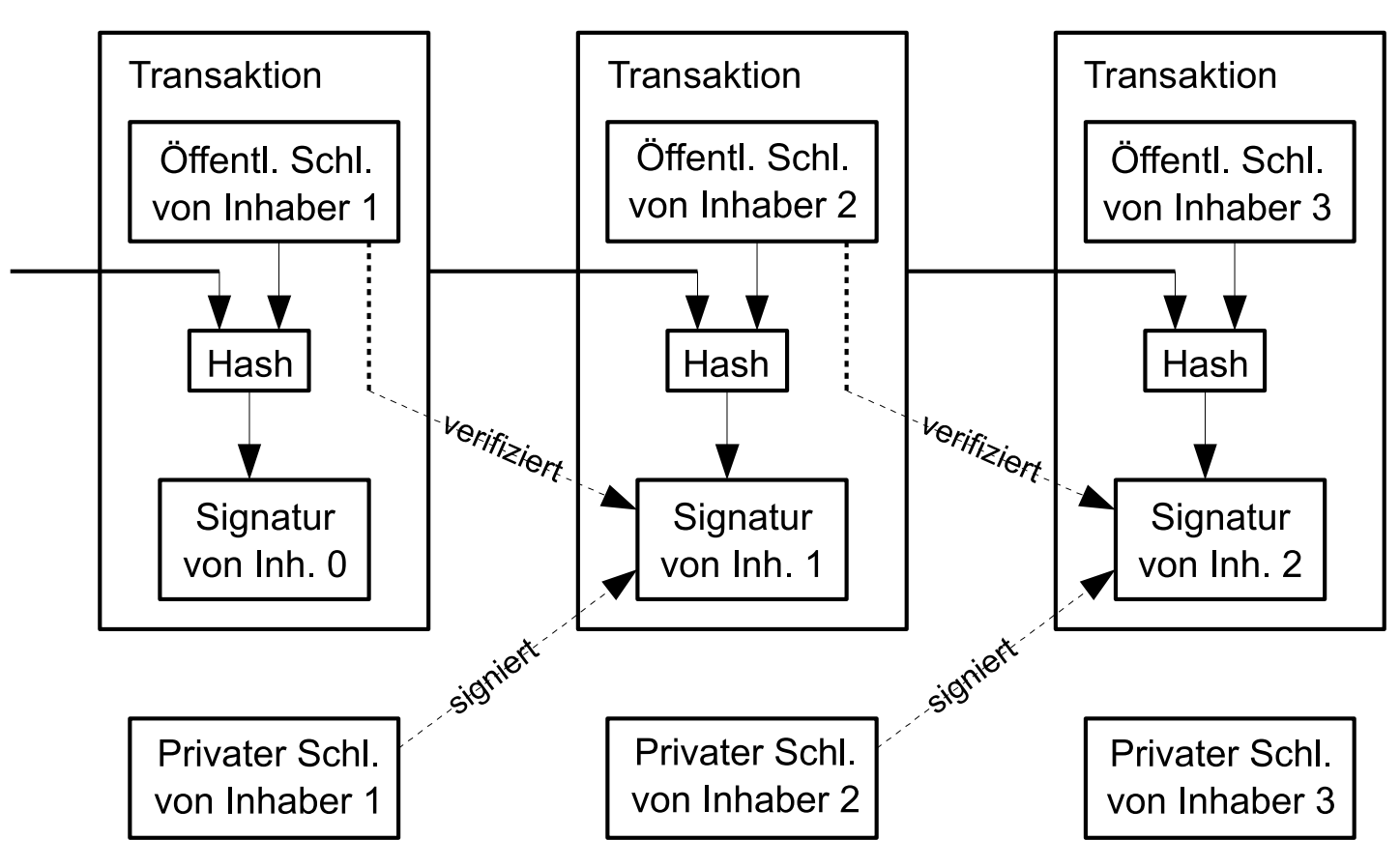
Wir definieren einen elektronischen Coin als eine Kette digitaler Signaturen. Jeder Besitzer transferiert den Coin zum nächsten, indem er einen Hashwert der vorherigen Transaktion sowie den öffentlichen Schlüssel des nächsten Besitzers digital signiert und beide dem Ende des Coins hinzufügt. Der Zahlungsempfänger kann die Signaturen verifizieren, um die Inhaberkette zu verifizieren.

Das Problem ist natürlich, dass der Zahlungsempfänger nicht verifizieren kann, dass keiner der vorherigen Besitzer den Coin zweimal ausgegeben hat. Eine herkömmliche Lösung ist das Hinzuziehen einer zentralen Autorität, oder Münzstätte, die jede Transaktion auf Doppelausgaben hin überprüft. Nach jeder Transaktion muss der Coin bei der Münzstätte abgeliefert werden, um einen neuen ausgeben zu lassen, und nur im Falle von Coins, die direkt von der Münzstätte stammen, ist Verlass darauf, dass sie nicht doppelt ausgegeben wurden. Das Problem mit dieser Lösung ist, dass das Schicksal des gesamten Geldsystems von dem Unternehmen abhängt, welches die Münzstätte betreibt, wobei jede Transaktion über dieses laufen muss, genau wie bei einer Bank.

Wir benötigen eine Möglichkeit, den Zahlungsempfänger wissen zu lassen, dass der vorherige Besitzer keine früheren Transaktionen signiert hat. Für unsere Zwecke ist die früheste Transaktion entscheidend, weshalb uns spätere Doppelausgabenversuche nicht kümmern. Die einzige Möglichkeit, die Abwesenheit einer Transaktion zu bestätigen, ist es, sich aller Transaktionen bewusst zu sein. Im Münzanstalt-basierten Modell wusste die Münzanstalt von allen Transaktionen und entschied, welche zuerst eintraf. Um das ohne eine vertrauenswürdige dritte Partei zu gewährleisten, müssen Transaktionen öffentlich bekannt gemacht werden [1], und wir brauchen ein System, durch das Teilnehmer sich auf einen einzigen Verlauf der Reihenfolge ihres Empfangs einigen können. Der Zahlungsempfänger benötigt einen Nachweis darüber, dass die Mehrheit der Nodes zum Zeitpunkt jeder Transaktion darin übereinstimmten, dass sie die zuerst empfangene war.

3. Zeitstempelserver

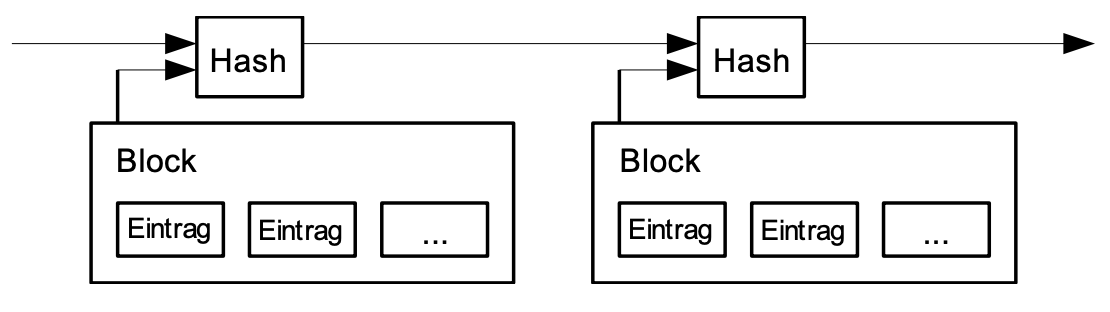
Die Lösung, welche wir vorschlagen, beginnt mit einem Zeitstempelserver. Ein Zeitstempelserver operiert, indem er einen Hashwert eines Blocks von Einträgen, die zeitgestempelt werden sollen, erzeugt und diesen weiträumig veröffentlicht, etwa in einer Zeitung oder einem Usenet-Beitrag [2-5]. Der Zeitstempel beweist, dass die Daten offensichtlicherweise zu diesem Zeitpunkt existiert haben müssen, um in den Hash zu gelangen. Jeder Zeitstempel schließt den vorherigen in seinen Hashwert ein und bildet so eine Kette, wobei jeder zusätzliche Zeitstempel die vorangegangenen bekräftigt.

4. Arbeitsnachweis

Um einen verteilten Zeitstempelserver auf Peer-to-Peer-Basis zu implementieren, werden wir statt Zeitungen oder Usenet-Beiträgen ein Arbeitsnachweissystem ähnlich dem von Adam Backs Hashcash [6] benötigen. Der Arbeitsnachweis involviert die Suche nach einem Wert, der, wenn er – beispielsweise mit SHA-256 – gehasht wird, mit einer Reihe von Null-Bits beginnt. Die durchschnittlich erforderliche Arbeit steigt mit der Anzahl der erforderlichen Null-Bits exponentiell an und kann durch das Ausführen einer einzigen Hashfunktion verifiziert werden.

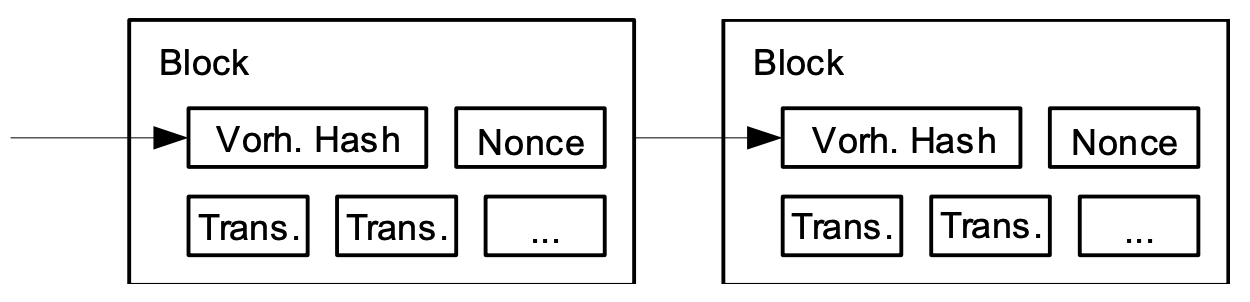
Wir implementieren den Arbeitsnachweis für unser Zeitstempelnetzwerk, indem wir eine Nonce im Block so lange erhöhen, bis ein Wert gefunden wird, welcher dem Block die notwendige Anzahl an Null-Bits gibt. Sobald die zur Bereitstellung des Arbeitsnachweises erforderliche CPU-Leistung aufgewandt wurde, kann der Block nicht geändert werden, ohne diese Arbeit erneut zu verrichten. Sobald spätere Blöcke nach ihm in die Kette aufgenommen werden, schlösse die Arbeit zur Änderung des Blockes die Wiedererzeugung aller auf ihn folgenden Blöcke ein.

Der Arbeitsnachweis löst außerdem das Problem der Repräsentation bei Mehrheitsentscheidungen. Würde die Mehrheit auf dem Prinzip einer Stimme pro IP-Adresse basieren, könnte sie durch jeden, der in der Lage ist, viele IP-Adressen bereitzustellen, untergraben werden. Der Arbeitsnachweis etabliert im Grunde genommen eine Stimme pro CPU. Die Mehrheitsentscheidung wird durch die längste Kette repräsentiert, in welche der größte Arbeitsnachweisaufwand investiert wurde. Wenn der Großteil der CPU-Leistung von aufrichtigen Nodes kontrolliert wird, wird die aufrichtige Kette am schnellsten wachsen und alle konkurrierenden Ketten hinter sich lassen. Um einen vergangenen Block zu ändern, müsste ein Angreifer die Arbeitsnachweise dieses Blockes und aller auf ihn folgenden Blocke erneut erbringen und dann die Arbeit der aufrichtigen Nodes ein- und überholen. Wir werden später zeigen, dass die Wahrscheinlichkeit, dass ein langsamerer Angreifer aufholt, exponentiell abnimmt, wenn weitere Blöcke hinzugefügt werden.

Um mit der Zeit zunehmende Hardwaregeschwindigkeit und fluktuierendes Interesse am Betrieb von Nodes auszugleichen, wird die Schwierigkeit des Arbeitsnachweises mittels eines gleitenden Durchschnitts bestimmt, der auf eine durchschnittliche Anzahl von Blöcken pro Stunde abzielt. Wenn sie zu schnell erzeugt werden, steigt die Schwierigkeit.

5. Netzwerk

Die Schritte für den Betrieb des Netzwerks sind folgende:

1. Neue Transaktionen werden an alle Nodes ausgestrahlt.
2. Jeder Node sammelt neue Transaktionen in einem Block.
3. Jeder Node arbeitet daran, einen schwierigen Arbeitsnachweis für seinen Block zu finden.
4. Wenn ein Node einen Arbeitsnachweis findet, strahlt er seinen Block an alle Nodes aus.
5. Nodes akzeptieren den Block nur, falls alle in ihm enthaltenen Transaktionen gültig und noch nicht ausgegeben sind.
6. Nodes drücken ihre Akzeptanz des Blockes dadurch aus, dass sie am nächsten Block in der Kette zu arbeiten beginnen und dabei den Hashwert des akzeptierten Blocks als vorherigen Hashwert benutzen.

Nodes sehen stets die längste Kette als die korrekte an und werden daran arbeiten, sie zu erweitern. Sollten zwei Nodes simultan verschiedene Versionen des nächsten Blocks ausstrahlen, könnten einige Nodes den einen oder anderen zuerst empfangen. In diesem Fall arbeiten sie an dem, welchen sie zuerst empfangen, aber speichern den anderen Zweig für den Fall, dass dieser länger wird. Der Gleichstand wird aufgehoben, wenn der nächste Arbeitsnachweis gefunden und einer der Zweige länger wird; die Nodes, welche am anderen Zweig arbeiteten, werden dann zum längeren wechseln.

Neu ausgestrahlte Transaktionen müssen nicht zwangsläufig alle Nodes erreichen. Solange sie viele Nodes erreichen, werden sie innerhalb kurzer Zeit in einen Block gelangen. Blockausstrahlungen sind außerdem gegen verlorengegangene Nachrichten resistent. Wenn ein Node einen Block nicht empfängt, wird er ihn anfragen, sobald er den nächsten Block empfängt und erkennt, dass er einen verpasst hat.

6. Anreiz

Der Konvention gemäß ist die erste Transaktion eines Blocks eine besondere Transaktion, welche einen neuen Coin beginnt, der dem Erzeuger des Blocks gehört. Dies schafft einen Anreiz für Nodes, das Netzwerk zu unterstützten, und stellt einen Distributionsmechanismus dar, der neue Coins in Umlauf bringt, da es keine zentrale Autorität gibt, welche sie ausgeben könnte. Der stetige Zufluss einer konstanten Menge neuer Coins gleicht der von Goldproduzenten, die Ressourcen dazu aufwenden, zusätzliches Gold in Umlauf zu bringen. In unserem Fall sind es CPU-Zeit und Strom, die aufgewendet werden.

Der Anreiz besteht zudem in Transaktionsgebühren. Wenn der Ausgangswert einer Transaktion geringer ist als der Eingangswert, besteht die Differenz aus einer Transaktionsgebühr, die dem Anreizwert des Blocks, welcher die Transaktion enthält, hinzugefügt wird. Sobald eine im Voraus festgelegte Anzahl an Coins in Umlauf gebracht wurde, kann der Anreiz gänzlich auf Transaktionsgebühren übergehen und vollständig inflationsfrei sein.

Der Anreiz mag dabei helfen, Nodes zur Ehrlichkeit zu ermutigen. Sollte ein gieriger Angreifer in der Lage sein, mehr CPU-Leistung als alle ehrlichen Nodes aufzubauen, müsste er bei ihrer Verwendung zwischen dem Betrug anderer durch das Zurückstehlen seiner Zahlungen und der Erzeugung neuer Coins wählen. Er sollte es als profitabler erachten, sich an die Regeln zu halten, die ihn mit mehr Coins begünstigen als allen anderen zusammengenommen, als das System und damit die Gültigkeit seines eigenen Reichtums zu untergraben.

7. Rückgewinnung von Speicherplatz

Sobald die letzte Transaktion in einem Coin unter einer ausreichenden Anzahl von Blöcken begraben ist, können die ausgegebenen Transaktionen vor ihr gelöscht werden, um Speicherplatz zu sparen. Um dies zu begünstigen, ohne den Hashwert des Blockes zu zerstören, werden Transaktionen in einen Hash-Baum [7][2][5] gehasht, wobei nur die Wurzel im Hashwert des Blockes einbegriffen ist. Alte Blöcke können dann durch das Stutzen der Zweige des Baumes kompakter gemacht werden. Die inneren Hashwerte müssen nicht gespeichert werden.

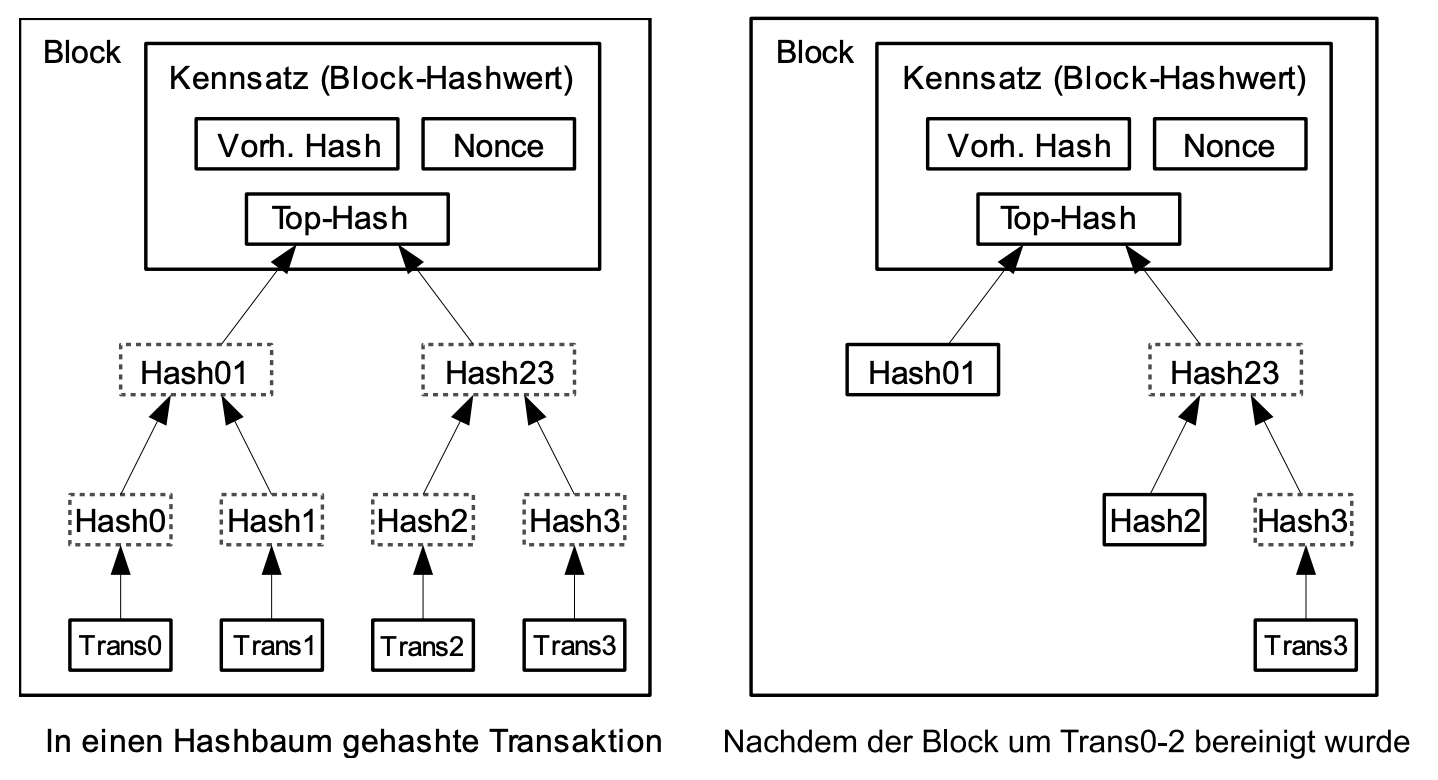
Der Kennsatz eines transaktionslosen Blockes würde etwa 80 Bytes umfassen. Wenn wir annehmen, dass Blöcke etwa alle 10 Minuten generiert werden, 80 Bytes * 6 * 24 * 365 = 4,2 MB pro Jahr. Bei einer typischen Ausstattung von im Jahr 2008 verkäuflicher Computersysteme mit 2 GB RAM und einem nach Moores Gesetz derzeit anzunehmenden Wachstum von 1,2 GB pro Jahr sollte Speicherplatz kein Problem sein, selbst wenn die Kennsätze von Blöcken gespeichert werden müssen.

8. Vereinfachte Zahlungsverifizierung

Es ist möglich, Zahlungen ohne den Betrieb eines Full Nodes zu überprüfen. Ein Nutzer muss lediglich die Kennsätze der längsten Arbeitsnachweiskette aufbewahren, welche er bei Nodes abfragen kann, bis er davon überzeugt ist, dass er die längste Kette besitzt, und den Hash-Baum-Zweig erhält, der die Transaktion mit dem Block, in welchem sie zeitgestempelt wurde, verbindet. Er kann die Transaktion nicht selbst überprüfen, aber indem er sie mit einem Ort in der Kette verknüpft, kann er sehen, dass ein Netzwerknode sie akzeptiert hat, wobei Blöcke, die nach ihm hinzugefügt wurden, zusätzlich bestätigen, dass das Netzwerk sie akzeptiert hat.

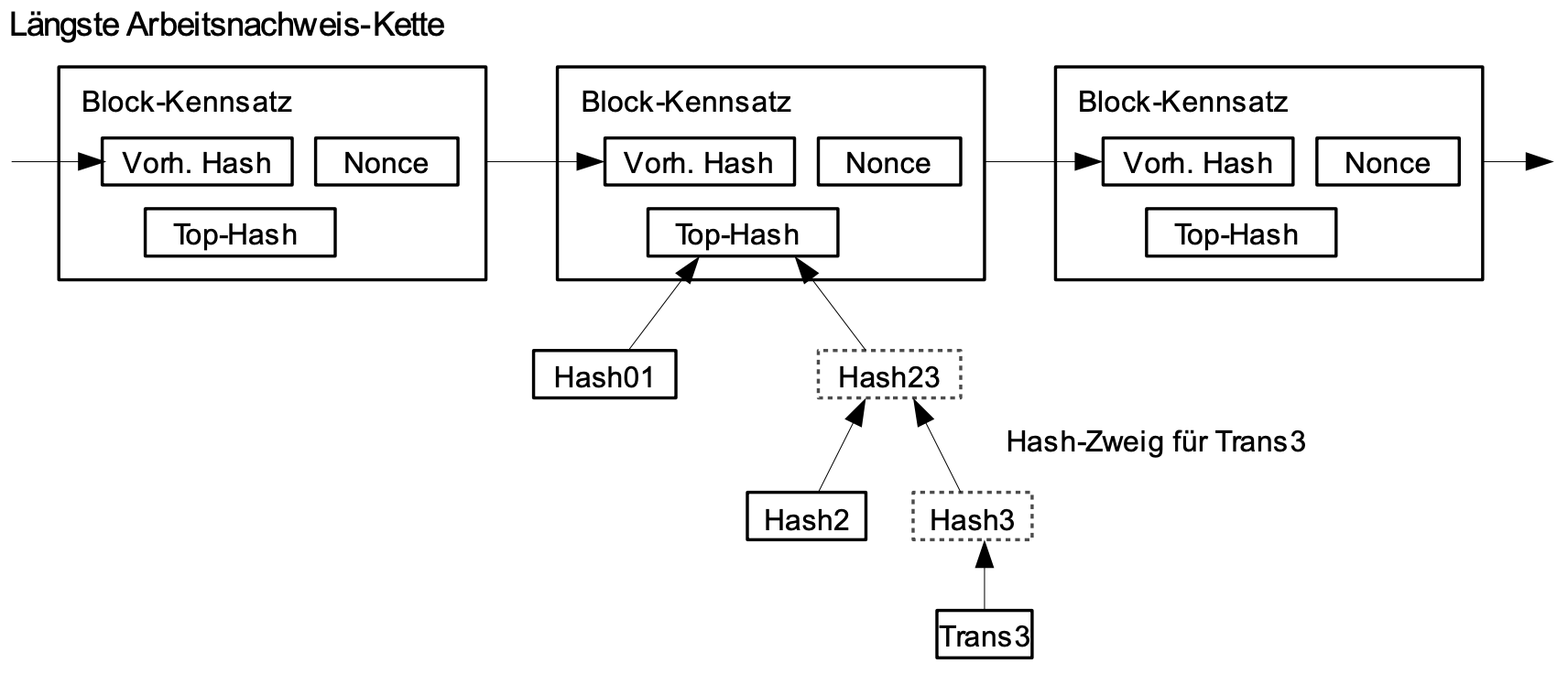
Somit ist die Überprüfung zuverlässig, solange aufrichtige Nodes das Netzwerk kontrollieren, aber gefährdeter, sollte das Netzwerk durch einen Angreifer überwältigt worden sein. Während Netzwerknodes dazu in der Lage sind Transaktionen selbst zu verifizieren, kann die vereinfachte Methode durch die gefälschten Transaktionen eines Angreifers überlistet werden, solange er das Netzwerk überwältigt. Eine Strategie zum Schutz davor wäre es, Warnmeldungen von Nodes anzunehmen, wenn diese einen ungültigen Block entdeckt haben, was die Software des Nutzers dazu aufforderte, den gesamten Block und die den Alarm auslösenden Transaktionen herunterzuladen, um die Inkonsistenz zu bestätigen. Unternehmen, die häufig Zahlungen entgegennehmen, würden wahrscheinlich zwecks größerer Unabhängigkeit ihrer Sicherheitsmaßnahmen und schnellerer Verifikation trotzdem ihre eigenen Nodes betreiben wollen.

9. Werte kombinieren und aufteilen

Obwohl es möglich wäre, Coins individuell zu handhaben, wäre es unpraktisch, für jeden Cent einer Überweisung separate Transaktionen zu tätigen. Um Werte kombinieren und aufspalten zu können, enthalten Transaktionen mehrere Ein- und Ausgänge. Normalerweise wird es entweder einen Eingang von einer größeren vorangegangenen Transaktion oder mehrere aus kleineren Beträgen zusammengesetzte, sowie höchstens zwei Ausgänge geben: einen für die Zahlung und einen, der eventuell anfallendes Wechselgeld zum Absender zurückschickt.

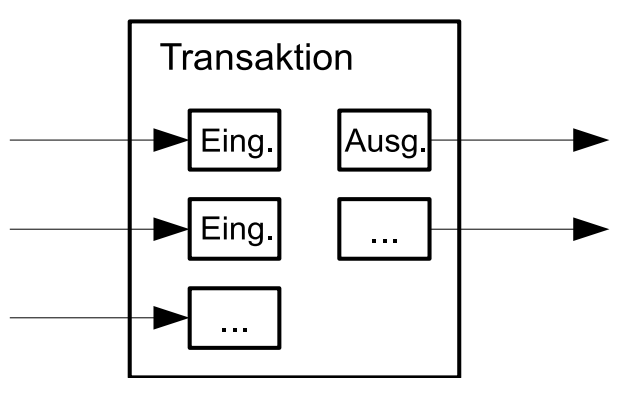
Es sollte angemerkt werden, dass die Auffächerung von Transaktionen, bei der eine Transaktion von mehreren anderen Transaktionen abhängt, welche wiederum von vielen weiteren abhängen, hier kein Problem darstellt. Es ist niemals vonnöten, den gesamten Verlauf einer Transaktion zu extrahieren.

10. Datenschutz

Das traditionelle Bankenmodell stellt ein gewisses Niveau an Datenschutz dadurch sicher, dass es der Zugang zu Informationen auf die involvierten Parteien und die vertrauenswürdige dritte Partei einschränkt. Die Notwendigkeit, alle Transaktionen öffentlich kundzugeben, schließt diesen Ansatz aus, doch Datenschutz kann dadurch aufrechterhalten werden, dass der Informationsfluss an anderer Stelle unterbrochen wird: indem öffentliche Schlüssel anonym gehalten werden. Die Öffentlichkeit kann sehen, dass jemand einen Betrag an jemand anderen schickt, aber ohne Informationen, welche die Transaktion mit irgendwem in Verbindung bringen. Dies ähnelt den von Aktienbörsen veröffentlichten Informationen, durch welche Zeitpunkt und Umfang individueller Händel, das „Band“, öffentlich gemacht werden, ohne die Parteien zu enthüllen.

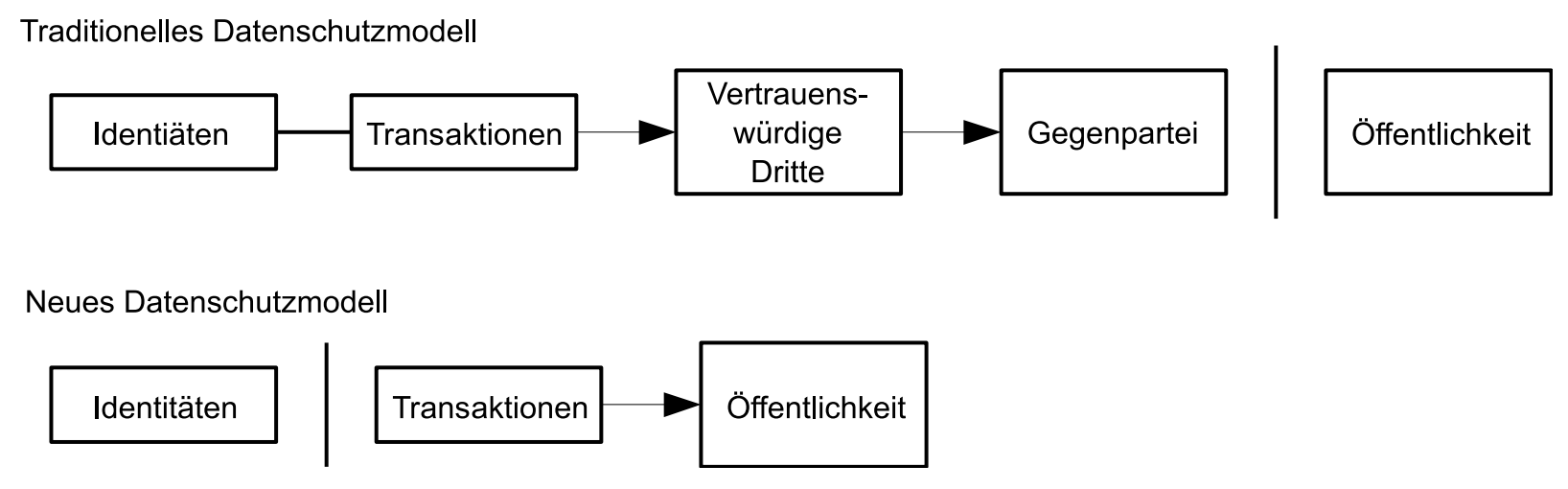
Als zusätzliche Firewall sollte für jede Transaktion ein neues Schlüsselpaar verwendet werden, um zu verhindern, dass sie in Beziehung zu einem gemeinsamen Besitzer gebracht werden können. Eine gewisse Assoziation ist bei Transaktionen mit mehreren Eingängen dennoch unausweichlich, da diese notwendigerweise enthüllen, dass die Eingänge von demselben Besitzer stammen. Das durch die Enthüllung eines Schlüsselbesitzers zustande kommende Risiko besteht darin, dass per Assoziation auch andere Transaktionen desselben Besitzers aufgedeckt werden könnten.

11. Berechnungen

Betrachten wir das eines Angreifers, der versucht, eine alternative Kette schneller als die ehrliche Kette zu generieren. Selbst im Falle eines Erfolges eröffnet dies nicht die Möglichkeit willkürlicher Änderungen am System, wie beispielsweise der Erzeugung von Wert aus dem Nichts oder der Beschlagnahmung von Geld, das dem Angreifer nie gehörte. Nodes werden keine ungültigen Transaktionen als Zahlungen akzeptieren und ehrliche Nodes werden niemals Blöcke akzeptieren, die sie enthalten. Ein Angreifer kann nur versuchen, eine seiner eigenen Transaktionen zu ändern und Geld, das er kürzlich ausgab, zurückzuholen.

Das Wettrennen zwischen aufrichtiger Kette und Angreifer kann als binominale zufällige Irrfahrt charakterisiert werden. Das Erfolgsereignis besteht darin, dass die ehrliche Kette um einen Block erweitert wird, was ihren Vorsprung um +1 erhöht, und das Fehlschlagsereignis besteht in der Erweiterung der Angreiferkette um einen Block, wodurch der Abstand um -1 reduziert wird.

Die Wahrscheinlichkeit, dass ein Angreifer von einem gegebenen Abstand aus aufholt, entspricht dem Ruin des Spielers-Problem. Nehmen wir an, dass ein Glücksspieler unbegrenzten Kredits mit einem Rückstand beginnt und potenziell unbegrenzt viele Züge in dem Versuch spielen kann, auf Null zu kommen. Wir können die Wahrscheinlichkeit, dass er Null erreicht oder dass ein Angreifer die ehrliche Kette jemals einholt, folgendermaßen berechnen [8]:

$p=$ Wahrscheinlichkeit, dass ein ehrlicher Node den nächsten Block findet
$q=$ Wahrscheinlichkeit, dass der Angreifer den nächsten Block findet
$q_{\mathrm{z}}=$ Wahrscheinlichkeit, dass der Angreifer jemals einen Rückstand von z Blöcken aufholt

Unsere Annahme, dass $p>q$, vorausgesetzt, nimmt die Wahrscheinlichkeit mit der Anzahl der Blöcke, die der Angreifer aufholen muss, exponentiell ab. Wenn er nicht früh einen glücklichen Sprung vorwärts macht, werden seine Chancen unter diesen widrigen Bedingungen verschwinden gering, während er weiter zurückfällt.

Nun erwägen wir, wie lange der Empfänger einer neuen Transaktion warten muss, bevor er sich ausreichend sicher sein kann, dass der Absender die Transaktion nicht mehr zu ändern imstande ist. Wir nehmen an, dass der Absender ein Angreifer ist, welcher dem Empfänger vorgaukeln will, dass er ihn vor einer Weile bezahlte, aber die Zahlung dann nach einem gewissen Zeitraum zu sich zurückleitet. Der Empfänger wird benachrichtigt, wenn das passiert, aber der Absender hofft, dass es dann bereits zu spät sein wird.

Der Empfänger generiert ein neues Schlüsselpaar und gibt dem Absender kurz vor der Signierung den öffentlichen Schlüssel. Dies hält den Absender davon ab, im Voraus eine Kette von Blöcken vorzubereiten und kontinuierlich an dieser zu arbeiten, bis er das Glück hat, weit genug in den Vorsprung zu gelangen, um dann in diesem Moment die Transaktion auszuführen. Sobald die Transaktion abgeschickt wurde, beginnt der unehrliche Absender im geheimen, an einer parallelen Kette zu arbeiten, welche die alternative Version seiner Transaktion enthält.

Der Empfänger wartet, bis die Transaktion zu einem Block hinzugefügt wurde und z Blöcke nach ihr aufgereiht sind. Er kennt das genaue Ausmaß des Fortschrittes nicht, den der Angreifer machte, doch vorausgesetzt, dass die ehrlichen Blöcke die zu erwartende durchschnittliche Zeit per Block in Anspruch nahmen, wird der potenzielle Fortschritt des Angreifers eine Poisson-Verteilung mit folgendem Erwartungswert sein:

Um die Wahrscheinlichkeit zu ermitteln, dass der Angreifer nun noch aufholen könnte, multiplizieren wir die Poisson-Dichte jedes Fortschrittes, den er gemacht haben könnte, mit der Wahrscheinlichkeit, dass er von diesem Punkt aus aufzuholen in der Lage ist:

Umgeformt, um die Summierung des unendlichen Randes der Verteilung zu vermeiden …

In C-Code konvertiert …

	#include <math.h>
	double AttackerSuccessProbability(double q, int z)
	{
		double p = 1.0 - q;
		double lambda = z * (q / p);
		double sum = 1.0;
		int i, k;
		for (k = 0; k <= z; k++)
		{
			double poisson = exp(-lambda);
			for (i = 1; i <= k; i++)
			poisson *= lambda / i;
			sum -= poisson * (1 - pow(q / p, z - k));
		}
		return sum;
	}
		

Wenn wir uns einige Resultate ausgeben lassen, können wir sehen, dass die Wahrscheinlichkeit mit $z$ exponentiell sinkt.

	q=0.1
	z=0		P=1.0000000
	z=1		P=0.2045873
	z=2		P=0.0509779
	z=3		P=0.0131722
	z=4		P=0.0034552
	z=5		P=0.0009137
	z=6		P=0.0002428
	z=7		P=0.0000647
	z=8		P=0.0000173
	z=9		P=0.0000046
	z=10	P=0.0000012
		

	q=0.3
	z=0		P=1.0000000
	z=5		P=0.1773523
	z=10	P=0.0416605
	z=15	P=0.0101008
	z=20	P=0.0024804
	z=25	P=0.0006132
	z=30	P=0.0001522
	z=35	P=0.0000379
	z=40	P=0.0000095
	z=45	P=0.0000024
	z=50	P=0.0000006
		

Für $P<\mathrm{0.1\%}$ …

	P < 0.001
	q=0.10	z=5
	q=0.15	z=8
	q=0.20	z=11
	q=0.25	z=15
	q=0.30	z=24
	q=0.35	z=41
	q=0.40	z=89
	q=0.45	z=340
		

12. Konklusion

Wir haben ein System für elektronische Transaktionen vorgeschlagen, das nicht auf Vertrauen beruht. Wir begannen mit dem herkömmlichen Ansatz von aus digitalen Signaturen bestehenden Coins, was eine starke Kontrolle der Inhaberschaft ermöglicht, aber ohne eine Möglichkeit, Doppelausgaben zu verhindern, unvollständig ist. Um dies zu lösen, schlugen wir ein Peer-to-Peer-Netzwerk vor, das Arbeitsnachweise dazu benutzt, einen öffentlichen Verlauf von Transaktionen aufzuzeichnen, dessen Veränderung durch Angreifer rasch unpraktikabel wird, solange ehrliche Nodes den Großteil der CPU-Leistung kontrollieren. Das Netzwerk ist robust in seiner unstrukturierten Einfachheit. Nodes arbeiten gleichzeitig und mit wenig Koordination. Sie müssen nicht identifiziert werden, da Nachrichten nicht zu einem bestimmten Ort geschickt und nur nach dem Prinzip bestmöglichen Bemühens zugestellt werden müssen. Nodes können das Netzwerk nach Gutdünken verlassen oder sich ihm anschließen, wobei sie die Arbeitsnachweiskette als Beweis dafür akzeptieren, was während ihrer Abwesenheit stattfand. Sie stimmen mit ihrer CPU-Leistung ab, wobei sie ihre Akzeptanz gültiger Blöcke dadurch zum Ausdruck bringen, indem sie daran arbeiten, sie zu erweitern und ungültige Blöcke dadurch ablehnen, dass sie sich weigern, an ihnen zu arbeiten. Alle notwendigen Regeln und Anreize können mit diesem Konsensmechanismus durchgesetzt werden.

Literaturverzeichnis

1. W. Dai, „b-money,“ http://www.weidai.com/bmoney.txt, 1998.
2. H. Massias, X.S. Avila, and J.-J. Quisquater, „Design of a secure timestamping service with minimal trust requirements,“ in: 20th Symposium on Information Theory in the Benelux, Mai 1999.
3. S. Haber, W.S. Stornetta, „How to time-stamp a digital document,“ in: Journal of Cryptology, Bd. 3, Nr. 2, S. 99-111, 1991.
4. D. Bayer, S. Haber, W.S. Stornetta, „Improving the efficiency and reliability of digital time-stamping,“ in: Sequences II: Methods in: Communication, Security and Computer Science, S. 329-334, 1993.
5. S. Haber, W.S. Stornetta, „Secure names for bit-strings,“ in: Proceedings of the 4th ACM Conference on Computer and Communications Security, S. 28-35, April 1997.
6. A. Back, „Hashcash – a denial of service counter-measure,“ http://www.hashcash.org/papers/hashcash.pdf, 2002.
7. R.C. Merkle, „Protocols for public key cryptosystems,“ in: Proc. 1980 Symposium on Security and Privacy, IEEE Computer Society, S. 122-133, April 1980.
8. W. Feller, „An introduction to probability theory and its applications,“ 1957.